Croissance exponentielle, confinement…On en parle Covid-19 oblige !

Aziz El Kacimi Alaoui (*)
L’imagination est la matière vitale de la littérature de fiction. Ses auteurs s’immergent dans le temps, en se tournant vers le passé ou en se projetant dans l’avenir. Ils s’adonnent à fabriquer des histoires fantastiques et folles mais aussi catastrophiques à nous plonger dans l’effroi. Elles appâtent ainsi les lecteurs friands de sensations extrêmes et de dépense d’adrénaline. Mais c’est seulement aux moments perdus où ils sont bien installés sur un canapé, assis sur un banc d’une gare ou un fauteuil d’aéroport… qu’ils atteignent l’état de transcendance dans lequel ces histoires les transportent. Ils tuent le temps avec et repartent vaquer à leurs occupations habituelles, comme si de rien n’était, loin d’imaginer qu’un jour ils seraient les acteurs – involontaires mais vrais – de ces scénarios irréels.
L’écrivain sud-africain Deon Meyer raconte dans son roman L’année du lion (paru en 2016) l’avènement d’une fièvre qui a décimé une grande partie de la race humaine. Un survivant s’en remit et tentait alors petit à petit de repartir à zéro en fondant une colonie pour reconstruire une humanité… L’Américaine Sylvia Browne (essayiste et médium) annonçait dans La fin des temps (son livre paru en 2008), l’arrivée d’une pneumonie qui allait toucher de plein fouet la totalité de notre planète-terre, en 2020 ! Comme c’est étrange : nous y sommes déjà ! ″Malheureusement pour elle″, l’auteure est décédée en 2013 et ne saura donc jamais que son imagination avait un contenu réel : c’est dire qu’une part de la fiction devient quelquefois une réalité impitoyable ! Alors, était-ce la prophétie d’une descendante de Nostradamus… ? Non ! les causes de la crise sanitaire que nous vivons sont purement naturelles, amplifiées certainement par le mode de vie désastreux que s’est choisi l’homme. (Une histoire que philosophes, sociologues, écolos, spécialistes de biodiversité…pourraient conter mieux que moi.) Mais, surtout, ce n’est nullement une sentence divine, comme certains tentaient de le faire croire.
Ce texte, quelque peu original par son contenu diversifié et sa forme tirée de toutes parts, a pour but d’exposer quelques ingrédients de mathématiques élémentaires destinés à un public non averti, souhaitant comprendre ce qui se dit par-ci par-là au sujet de la propagation du Coronavirus à laquelle nous sommes confrontés. Il ne faut le considérer que sous cet angle : en aucun cas, il ne prétend apporter quelque prévision que ce soit sur l’évolution future de la pandémie. Il est écrit de façon libre et ne répond pas aux attentes – certainement légitimes – de ceux qui ont la manie de toujours ranger les choses dans des cases ; ceux-là peuvent tout simplement zapper !
C’est en Chine, dans la ville de Wuhan, que naquit le monstre microscopique, tout au moins c’est là qu’il a été déclaré en premier. Les images que nous en offrait la presse (audiovisuelle plus particulièrement) étaient horribles. Elles semblaient tellement loin et ne nous amenaient guère à penser que nous pourrions un jour être nous-mêmes dans une telle réalité. C’est oublier la fameuse question de Edward Lorenz (précurseur de la théorie du chaos) posée en 1972 à un congrès scientifique : « Le battement d’ailes d’un papillon au Brésil peut-il provoquer une tornade au Texas ? ». Question fondamentale sur laquelle des mathématiciens de taille ont apporté des contributions substantielles mais où il reste encore à faire. L’un de ses aspects est la notion de croissance cumulée (éventuellement de l’erreur) : une machine qui peut fabriquer du gigantesque à partir du peu. Et en tête, un type particulier de cette croissance dont on entend parler de temps en temps, et beaucoup plus en ce moment :
La croissance exponentielle.
On raconte qu’à une époque de l’histoire, un roi en Inde nommé Shirham demanda à son sage Sissa de lui inventer un jouet qui lui permettrait de passer le temps. Ce dernier lui fabriqua un jeu d’échec. « Super ! s’exclama le roi. Que désires-tu comme récompense, Sissa ? – Une petite chose, Majesté ! lui répondit Sissa, poliment et en exécutant la petite courbette qu’il lui devait habituellement. – Demande ce que tu veux, voyons ! – Ce que je veux ? Juste remplir les cases de l’échiquier en respectant la règle qui suit : un grain de riz sur la première, deux sur la deuxième, quatre sur la troisième, huit sur la quatrième…et à chaque case, le double de celle qui la précède ! – Entendu ! lui promit le roi. » Il ordonna alors à ses valets de donner suite à la requête de Sissa, ne se doutant nullement où cela allait les amener. Pour éviter au lecteur hardi tout calcul épuisant, voici le nombre de grains de riz nécessaires pour remplir la 64ème case : 9 223 372 036 854 775 808 ainsi que celui de toutes les cases de l’échiquier : 18 446 744 073 709 551 615. Il paraît que les stocks de blé de tout le royaume ne suffirent pas à venir à bout du problème. De façon évidente, ce sont des nombres astronomiques dont la lecture seule exige du souffle !
Le jeu des puissances. Prenons un entier naturel a, c’est-à-dire un nombre choisi dans l’ensemble {0,1,2,3,4,5,6,…} (liste infinie). Si on le multiplie par lui-même, on obtient le nombre « a fois a » qu’on note a2, puis on multiplie ce dernier par a, pour obtenir « a fois a fois a » qu’on note a3, et ainsi de suite…À l’étape n de ce processus, on arrive à un nombre qu’on note an et qu’on lit « a à la puissance n » : c’est a multiplié par lui-même n fois. De façon évidente, on a toujours an=0 pour a=0 et an = 1 pour a=1, et ceci quelle que soit la valeur de l’entier n dans {1,2,3,4,5,6,…}. (Les mathématiciens conviennent – de façon justifiée bien sûr, mais que nous laissons de côté ici – que an =1, pour a=0 et n=0.) Par exemple, si on pend a=2 et n=63, on retrouve le nombre de grains de riz de la case 64 de l’échiquier de Sissa.
Ce jeu de puissances qui croissent de façon rapide pour atteindre de très grandes valeurs est similaire à celui qui régit la dynamique de progression d’une épidémie telle que celle qui sévit actuellement dans le monde. Si, pour faire simple, on suppose qu’en moyenne un sujet atteint contamine deux sujets saints, on peut schématiser la progression par le diagramme ci-dessous.
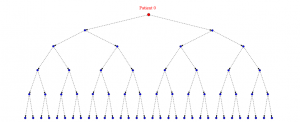
On voit qu’à la cinquième étape, le nombre de nouveaux contaminés (qu’on notera X) est déjà égal à 32. Cela semble a priori peu au début mais on a vu ce que ça donne au bout d’un nombre assez grand d’étapes : par exemple à l’étape 10, on a X=1024 et à l’étape 20, X=1 048 576. C’est à peu près la vitesse de propagation du Covid-19 constatée : le nombre de nouveaux contaminés double tous les trois jours (et 3 jours constituent ce que j’entendais par une étape dans le processus). L’étape 20 correspond à 60 jours et donc, si rien n’est entrepris pour stopper la maladie, le nombre de nouveaux contaminés, en partant initialement de deux, s’élèvera au bout de cette période à 220 = 1 048 576 ; par suite, le nombre total de contaminés dans la même période sera (par un calcul mathématique connu : somme des premiers termes d’une suite géométrique) de 2 097 151. Ce qui est considérable et, bien sûr, rudement inquiétant !
L’exponentielle. Le nombre X dépend de n et est une version d’une fonction mathématique bien connue appelée exponentielle : à la variable t (généralement désignant le temps), elle associe le nombre (on dit aussi la grandeur) qu’on note et. (e est un nombre positif appelé constante de Néper et valant approximativement 2,71828.) Les variantes de cette fonction sont du même type, par exemple la fonction at où a est n’importe quel nombre strictement positif (entier, fractionnaire, irrationnel…). La croissance rapide de ces fonctions a été mise en évidence pour la première fois au 18ème siècle par l’éminent mathématicien suisse Leonhard Euler (et comme par hasard, en travaillant sur la mortalité et la multiplication du genre humain). Le dessin qui suit représente le graphe de X= et. On y a choisi la même unité pour mesurer aussi bien la variable t que la grandeur X afin de visualiser de façon réelle la teneur de l’explosion de cette dernière.
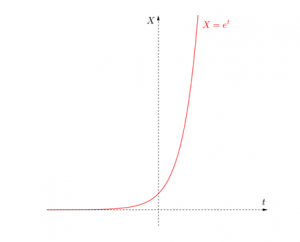
En réalité, les estimations qui ont été faites montrent qu’une personne infectée par de Covid-19 le transmet, en moyenne, à 3,6 autres (ce qui donne encore des estimations nettement supérieures à celles de l’exemple que nous avons pris). Alors que faire pour casser ces chaînes de transmission ? Dans l’impossibilité actuelle de disposer d’un traitement bien confirmé, l’un des moyens les plus efficaces est :
Le confinement
La définition qu’en donne le dictionnaire n’est pas exactement celle qu’on entend ces jours-ci. Pour tout le monde, cela signifie : « rester dans un endroit, bien isolé, bordé, sans possibilité de contact avec autrui ». Il a été constaté qu’à une distance d’au moins 1m50 d’une personne atteinte du virus, la contamination est très peu probable. D’où la nécessité de maintenir les individus d’une population, vivant dans un espace donné, à une telle distance l’un de l’autre. C’est ce qu’on appelle la distanciation sociale. Une manière d’opérer est d’obliger ces individus à rester chez eux : c’est le confinement. Sur le dessin qui suit, la patate est un espace de vie (une ville, un pays…) ; les individus y sont représentés par des points, au centre d’un disque dont le rayon est la distance prescrite, en l’occurrence 1m50 ou même 2m pour plus de sécurité : les verts sont les sujets saints et les rouges les sujets contaminés ; on y voit aussi un cluster constitué en grande partie de sujets infectés (regroupés comme par exemple pendant la cérémonie religieuse qui a eu lieu à Mulhouse en France).
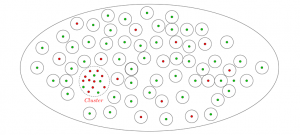
La réponse topologique à la pandémie !
Ici le confinement n’est pas total, il faut encore briser le cluster
Il est évident que la transmission n’a aucune chance de s’opérer pendant tout le confinement. D’où la nécessité de le maintenir jusqu’à ce que l’épidémie commence à être sérieusement jugulée, et ceci de manière clairement observable. Mais c’est toujours difficile d’imposer de telles contraintes à une population dont le nombre d’individus se compte par dizaines de millions avec, comme personne ne l’ignore, toutes les disparités entre les groupes que ce soit au niveau social, celui du mode de vie ou autres. Mais écoutons ce qu’en disent Diderot et d’Alembert dans leur encyclopédie : « Quand il s’agit du bien public, il est du devoir de la partie pensante de la nation d’éclairer ceux qui sont susceptibles de lumière, et d’entrainer par le poids de l’autorité cette foule sur qui l’évidence n’a point de prise. » Les deux penseurs semblent faire fi de toutes ces contraintes et ne prennent en compte que le danger réel – de mort ! – qui guette la communauté. Et donc, pas de liberté individuelle : dans une telle conjoncture, elle devient une liberté collective !
En guise d’épilogue
Dans le roman de Colette Dialogues de bêtes, Kiki-La-Doucette et Toby-Chien racontent leur vie quotidienne et le rapport qu’ils ont, tendre ou méchant, avec leur couple-maître qu’ils appellent communément Elle et Lui. Elle et Lui les regardent toujours d’en haut, pensant que rien ne se passe dans la tête de ces êtres minuscules. Tout comme ces deux bêtes, Corona, qui fait partie d’un monde carrément infinitésimal, nous observe aussi de la même façon, sans que nous nous en doutions un seul instant. Il joue le rôle principal dans la tragédie que nous vivons et a sûrement des choses à nous raconter. Alors pourquoi ne pas lui donner la parole ? Écoutons-le, c’est lui qui parle :
En observant longuement les humains
Des pensées terribles me saisissent.
Sur leurs déboires, sur leurs atrocités.
L’homme qui détruit l’homme :
L’exploitant à mort, le soumettant,
Le maintenant délibérément dans l’ignorance,
Et dans la sauvagerie : il le met dedans,
Le confine derrière des murs de plomb.
La cupidité constante des hommes,
Leur colle constamment à la peau !
L’injustice, ils s’en délectent.
L’égoïsme, ils s’y enferment.
L’injure, ils la profèrent sans limite.
La mégalomanie les ronge chaque jour :
Vouloir être le premier, cumuler !
Ils ont l’amour des grands chiffres :
Tous nos petits richards,
L’année un, ils se font un milliard,
Et l’année deux, vingt milliards !
Leur temps, ils le passent à racler
Sans qu’ils ne cessent d’avaler
Champagne et caviar !
Rassurez-vous : sans trop se larguer
Ils peuvent toujours se targuer
De se faire passer pour des pros
Avec leurs tonnes d’euros !
Ils détruisent les richesses naturelles :
Les terres qui les nourrissent,
Y bâtissent immeubles et gratte-ciels !
Ils tuent les arbres, les plantes, les fleurs…
Ils tuent la beauté et détruisent nos rêves !
L’homme n’est qu’un fanfaron,
Qui, toujours ne cesse de répéter :
Que cela ne se reproduise !
Mais il oublie et il recommence.
« Nous évoluons vers l’homme. »
Disait un grand philosophe !
Il s’appelait Jean-Paul Sartre.
Et bien non, il s’est trompé !
Corona s’essouffle, il fait une pause. Et reprend…
Quelle différence y a-t-il entre l’homme et celui qu’on appelle l’animal (pour le reléguer au second plan) ? Le premier a, paraît-il, un cerveau et réfléchit. Mais rarement pour le bien. Le deuxième est féroce : il se bat pour sa nourriture. Mais une fois qu’il l’a arrachée et s’est rassasié, il laisse le reste aux autres. Il n’emporte rien. Il ne cumule pas. L’homme, non ! il se satisfait et ne donne jamais ce qu’il a de trop. Il garde tout. S’il a de l’or, des diamants, des milliards, des richesses inouïes… et la possibilité d’en avoir encore, il prend. Alors qui est l’homme et qui est l’animal ?
Laissons parler un autre maître, lui aussi, il sait en dire… !
« Ils acquièrent des richesses et en deviennent plus pauvres. Ils veulent la puissance et tout d’abord le levier de la puissance, beaucoup d’argent – ces impuissants. »
Friedrich Nietzsche (Ainsi parlait Zarathoustra)
Des liens qui peuvent intéresser :
Épidémie : Peste de Marseille Une histoire réelle, bien contée, montrant le désastre auquel peut mener la cupidité des hommes. Elle va dans le sens de la chronique de Corona !
Dossier Épidémies sur le site Images des mathématiques du CNRS. Des articles de mathématiques dont certains sont accessibles à quidam.
(*) Aziz EL KACIMI ALAOUI est Professeur émérite (Mathématiques)
Université Polytechnique Hauts-de-France







